一、填空题(共15题,每题4分。共60分)
图1
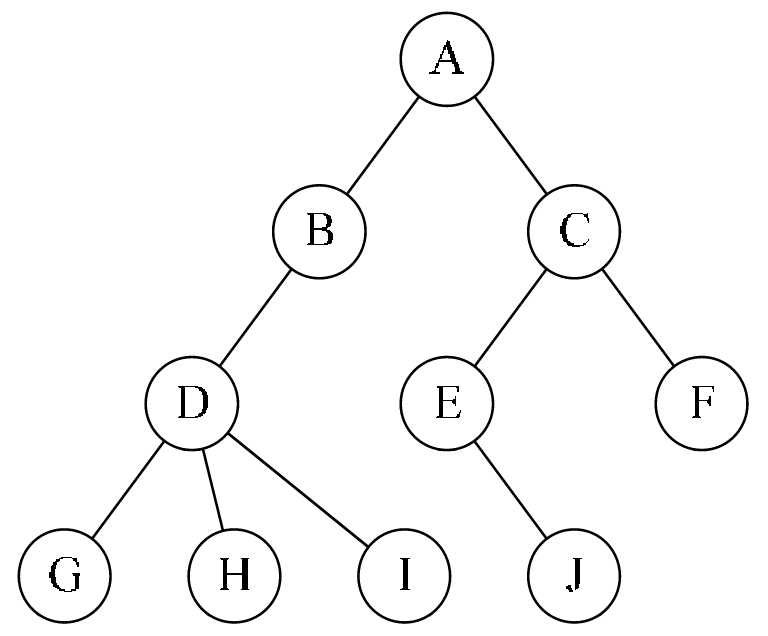 图2
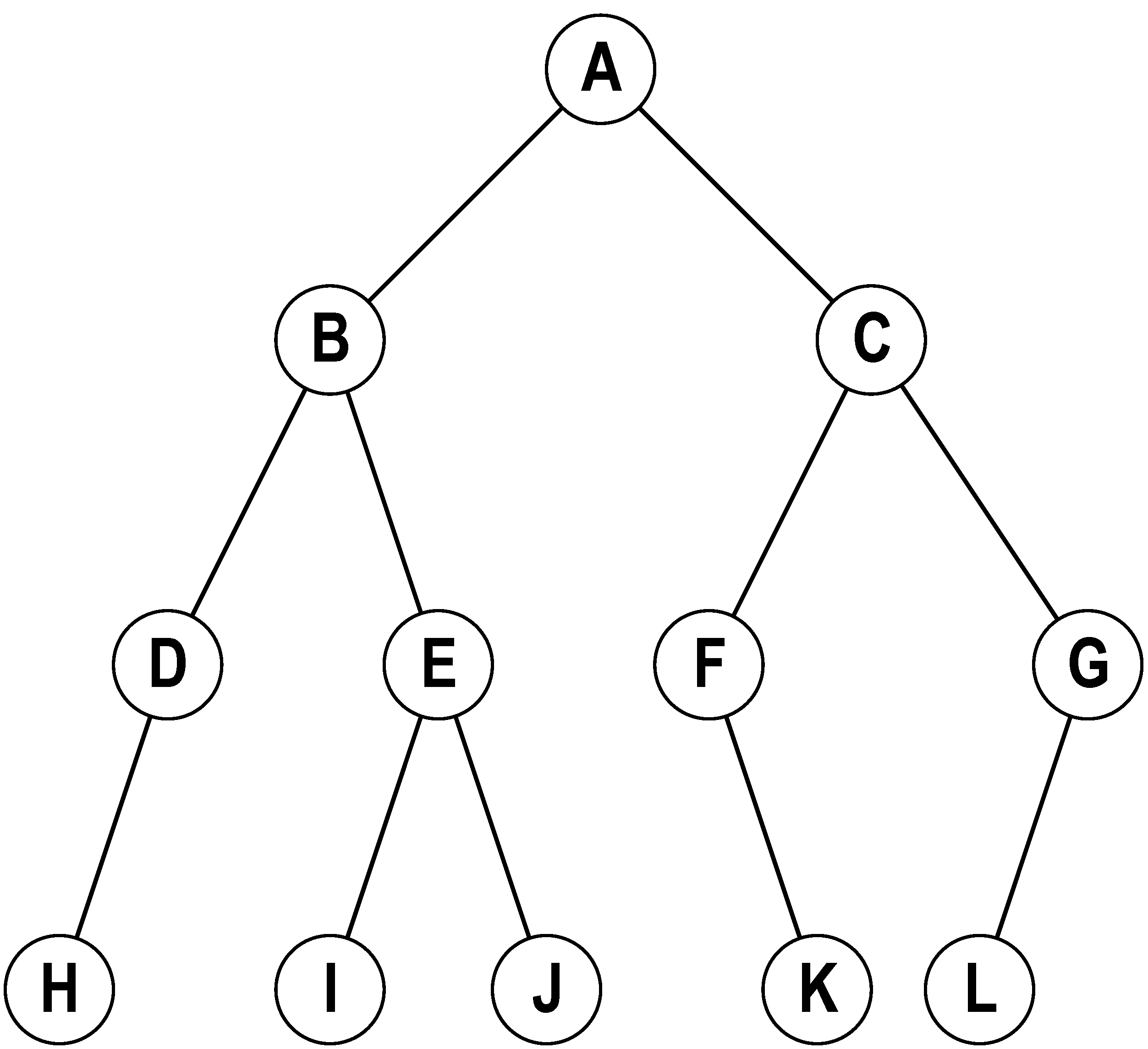
图2
-
一颗有N个节点的树一共有____条边.
-
在树的数据结构中,我们把没有子节点的节点称为树叶,那么图1中的树叶有____;具有相同父节点的节点互为兄弟节点,那么图1中E节点的兄弟节点有____.
-
从节点\({n}_{i}\)到\({n}_{k}\)的路径定义为节点\({n}_{1}\),\({n}_{2}\),…,\({n}_{k}\)的一个序列,使得对于\(1\le i < k\)的的节点\({n}_{i}\)是\({n}_{i+1}\)的父亲。该路径的长为该路径上边的条数,即____.
-
对任意节点\({n}_{i}\),\({n}_{i}\)的深度为从根到\({n}_{i}\)的唯一路径长,那么如图1,节点H的深度为____. \({n}_{i}\)的高是从\({n}_{i}\)到一个树叶的最长路经长,那么如图1,节点B的高为____.
-
定义一颗树的高为根节点的高,一棵树的深度为最深的树叶的深度,因此一棵树的高总是____.(大于,小于或等于)它的深度。
-
根据第3题中树的路径的定义,那么图1中节点D与节点C是否存在一条路径____(是或否).节点B与节点I是否存在一条路径____(是或否).
-
一棵树的深度是衡量一棵树优劣的重要指标,直接影响查找的时间复杂度,树越深平均查找时间复杂度越大。那么具有N个节点的树,最坏情况下其深度为____.
-
如图2,我们把每个节点都不多于两个儿子的树称为____树。
-
在二叉树中,深度为\(k\)的节点不超过____个.
-
高度为 \(h\) 的二叉树最多包含 ____个节点.反之由 \(n\) 个节点构成的二叉树,高度至少为____.
-
如图2的二叉树先序遍历序列为____,后序遍历序列为____.
-
对于一棵二叉树,如果对于树中的每个节点\(X\),它的左子树中的所有节点的值小于\(X\),而它的右子树中的所有节点的值大于\(X\),我们称这样的树为二叉查找树。如果我们用集合\(\left\{ 12,8,3,21,10,9,2 \right\}\)中的元素构造一颗二叉查找树,为了构造一棵最理想的二叉查找树,那么我们最好选择____作为树的根节点。这棵最理想的二叉查找树的高度为____.
-
如果要向一棵查找二叉树\(T\)中插入一个元素\(X\),只需将\(X\)与\(T\)的根节点比较,如果\(X\)小于根节点,那么继续将\(X\)与根节点的左子树的根节点比较,以此类推,直到找到一个叶子节点的位置将\(X\)插入为止。如果\(X\)大于根节点,那么继续将\(X\)与根节点的右子树的根节点比较,以此类推,直到找到一个叶节点的位置将\(X\)插入为止。那么我们依次将元素\(\left\{ 4,5,7,6 \right\}\)插入到第12题构造的理想二叉查找树中,这时该二叉查找树的高度将是____.
-
将所有元素\(\left\{ 12,8,3,21,10,9,2,4,5,7,6 \right\}\)构造一棵查找二叉树,理想高度应该是____.
-
定义树中一个节点的度为该节点的儿子节点个数。如果一棵深度为\(k\)的二叉树上只有度为0和度为2的节点,那么该树中包含的节点数至少为____.
二、解答题(共4题,每题10分。共40分)
-
我们称一颗二叉树中的满节点是具有两个儿子的节点。请证明在一颗非空二叉树中,树叶的个数总是比满节点多一个。
-
根据查找二叉树的定义,请画出包含且只包含节点\(\left\{ 12,8,3 \right\}\)的所有查找二叉树。
-
已知一棵二叉树的中序遍历序列为 cbafehgd,后序遍历序列为 cbfhgeda,请试着画出此二叉树。
-
通过填空题第12、13和14题我们可以看出,对于一棵理想的查找二叉树,我们不断向该树中插入新的元素,有可能会破坏该树的平衡,导致该树不再是所有节点构成的查找二叉树的理想型。对于查找二叉树的这种插入操作对树的平衡的破坏,尝试给出你的解决方案和实现思路来保证插入操作不会破坏树的平衡。
